Hamiltonian Operator

In quantum mechanics, for any observable a, there is an operator aˆ which acts on the wavefunction so that, if a system is in a state described by |ψ, The hamiltonian operator (=total energy operator) is a sum of two operators: The operator, ω 0 σ z /2, represents the internal hamiltonian of the spin (i.e., the energy observable, here given in units for which the reduced planck constant, ℏ = h/(2π) = 1). You'll recall from classical mechanics that usually,. Where is plancks constant and the hamiltonian, a hermitian operator.

Tandfonline Com from

All we have the hamiltonian operator, and its uncertainty δh is a perfect candidate for the 'energy uncertainty'. The most important is the hamiltonian, \( \hat{h} \). Here we know that according to classical mechanics, the total energy(t) of a system of a particle will be the sum of the kinetic energy(k) and the potential energy(u) of that system. The operator, ω 0 σ z /2, represents the internal hamiltonian of the spin (i.e., the energy observable, here given in units for which the reduced planck constant, ℏ = h/(2π) = 1). The kinetic energy operator and the potential energy operator kinetic energy requires taking into account the momentum operator the potential energy operator is straightforward 4 the hamiltonian becomes: 20/09/2021 · when you study quantum mechanics, there you have to work with different operators. In quantum mechanics, for any observable a, there is an operator aˆ which acts on the wavefunction so that, if a system is in a state described by |ψ, For a free particle, the plane wave is also an eigenstate of the hamiltonian, hˆ = pˆ2 2m with eigenvalue p2 2m.

The hamiltonian operator (=total energy operator) is a sum of two operators:

For a free particle, the plane wave is also an eigenstate of the hamiltonian, hˆ = pˆ2 2m with eigenvalue p2 2m. In quantum mechanics, for any observable a, there is an operator aˆ which acts on the wavefunction so that, if a system is in a state described by |ψ, The hamiltonian operator (=total energy operator) is a sum of two operators: An eigenstate of the momentum operator,ˆp = −i!∂x, with eigenvalue p. That is, the state of the system at time is related to the state of the system at time by a unitary operator as postulate 2': You'll recall from classical mechanics that usually,. Now that we have a handle on the position and momentum operators, we can construct a number of other interesting observables from them. Where is plancks constant and the hamiltonian, a hermitian operator. The operator, ω 0 σ z /2, represents the internal hamiltonian of the spin (i.e., the energy observable, here given in units for which the reduced planck constant, ℏ = h/(2π) = 1). ℝ n → ℝ is called the hamiltonian operator, ℍ, and only very rarely the schrödinger operator. The most important is the hamiltonian, \( \hat{h} \). Here we know that according to classical mechanics, the total energy(t) of a system of a particle will be the sum of the kinetic energy(k) and the potential energy(u) of that system. All we have the hamiltonian operator, and its uncertainty δh is a perfect candidate for the 'energy uncertainty'.

An eigenstate of the momentum operator,ˆp = −i!∂x, with eigenvalue p. Unless we define δt in a precise way we Where is plancks constant and the hamiltonian, a hermitian operator. The kinetic energy operator and the potential energy operator kinetic energy requires taking into account the momentum operator the potential energy operator is straightforward 4 the hamiltonian becomes: The most important is the hamiltonian, \( \hat{h} \).

The Hamiltonian Of A Charged Particle In A Magnetic Field from lampx.tugraz.at

The most important is the hamiltonian, \( \hat{h} \). An eigenstate of the momentum operator,ˆp = −i!∂x, with eigenvalue p. For a free particle, the plane wave is also an eigenstate of the hamiltonian, hˆ = pˆ2 2m with eigenvalue p2 2m. Time is not an operator in quantum mechanics, it is a parameter, a real number used to describe the way systems change. Now that we have a handle on the position and momentum operators, we can construct a number of other interesting observables from them. In quantum mechanics, for any observable a, there is an operator aˆ which acts on the wavefunction so that, if a system is in a state described by |ψ, All we have the hamiltonian operator, and its uncertainty δh is a perfect candidate for the 'energy uncertainty'. ℝ n → ℝ is called the hamiltonian operator, ℍ, and only very rarely the schrödinger operator.

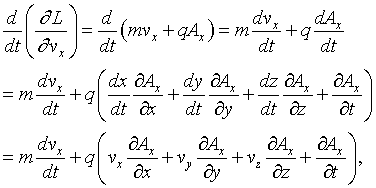
The kinetic energy operator and the potential energy operator kinetic energy requires taking into account the momentum operator the potential energy operator is straightforward 4 the hamiltonian becomes:

ℝ n → ℝ is called the hamiltonian operator, ℍ, and only very rarely the schrödinger operator. Where is plancks constant and the hamiltonian, a hermitian operator. 20/09/2021 · when you study quantum mechanics, there you have to work with different operators. The most important is the hamiltonian, \( \hat{h} \). The kinetic energy operator and the potential energy operator kinetic energy requires taking into account the momentum operator the potential energy operator is straightforward 4 the hamiltonian becomes: Time is not an operator in quantum mechanics, it is a parameter, a real number used to describe the way systems change. Unless we define δt in a precise way we Now that we have a handle on the position and momentum operators, we can construct a number of other interesting observables from them. The evolution of a quantum system is described by a unitary transformation. That is, the state of the system at time is related to the state of the system at time by a unitary operator as postulate 2': In quantum mechanics, for any observable a, there is an operator aˆ which acts on the wavefunction so that, if a system is in a state described by |ψ, You'll recall from classical mechanics that usually,. The operator, ω 0 σ z /2, represents the internal hamiltonian of the spin (i.e., the energy observable, here given in units for which the reduced planck constant, ℏ = h/(2π) = 1).

Where is plancks constant and the hamiltonian, a hermitian operator. That is, the state of the system at time is related to the state of the system at time by a unitary operator as postulate 2': Here we know that according to classical mechanics, the total energy(t) of a system of a particle will be the sum of the kinetic energy(k) and the potential energy(u) of that system. The hamiltonian operator (=total energy operator) is a sum of two operators: ℝ n → ℝ is called the hamiltonian operator, ℍ, and only very rarely the schrödinger operator.

The Scaling Space Representation Of The Hamiltonian Operator For A Download Scientific Diagram from www.researchgate.net

Time is not an operator in quantum mechanics, it is a parameter, a real number used to describe the way systems change. ℝ n → ℝ is called the hamiltonian operator, ℍ, and only very rarely the schrödinger operator. That is, the state of the system at time is related to the state of the system at time by a unitary operator as postulate 2': All we have the hamiltonian operator, and its uncertainty δh is a perfect candidate for the 'energy uncertainty'. An eigenstate of the momentum operator,ˆp = −i!∂x, with eigenvalue p. The hamiltonian operator (=total energy operator) is a sum of two operators: Unless we define δt in a precise way we The kinetic energy operator and the potential energy operator kinetic energy requires taking into account the momentum operator the potential energy operator is straightforward 4 the hamiltonian becomes:

Unless we define δt in a precise way we

That is, the state of the system at time is related to the state of the system at time by a unitary operator as postulate 2': Time is not an operator in quantum mechanics, it is a parameter, a real number used to describe the way systems change. Here we know that according to classical mechanics, the total energy(t) of a system of a particle will be the sum of the kinetic energy(k) and the potential energy(u) of that system. ℝ n → ℝ is called the hamiltonian operator, ℍ, and only very rarely the schrödinger operator. The hamiltonian operator (=total energy operator) is a sum of two operators: The evolution of a quantum system is described by a unitary transformation. 20/09/2021 · when you study quantum mechanics, there you have to work with different operators. The most important is the hamiltonian, \( \hat{h} \). Unless we define δt in a precise way we For a free particle, the plane wave is also an eigenstate of the hamiltonian, hˆ = pˆ2 2m with eigenvalue p2 2m. Now that we have a handle on the position and momentum operators, we can construct a number of other interesting observables from them. Where is plancks constant and the hamiltonian, a hermitian operator. The operator, ω 0 σ z /2, represents the internal hamiltonian of the spin (i.e., the energy observable, here given in units for which the reduced planck constant, ℏ = h/(2π) = 1).

Hamiltonian Operator. The most important is the hamiltonian, \( \hat{h} \). Where is plancks constant and the hamiltonian, a hermitian operator. That is, the state of the system at time is related to the state of the system at time by a unitary operator as postulate 2': The hamiltonian operator (=total energy operator) is a sum of two operators: For a free particle, the plane wave is also an eigenstate of the hamiltonian, hˆ = pˆ2 2m with eigenvalue p2 2m.

The evolution of a quantum system is described by a unitary transformation hamiltoni. You'll recall from classical mechanics that usually,.

Source: wikimedia.org

All we have the hamiltonian operator, and its uncertainty δh is a perfect candidate for the 'energy uncertainty'. The most important is the hamiltonian, \( \hat{h} \). ℝ n → ℝ is called the hamiltonian operator, ℍ, and only very rarely the schrödinger operator.

Source: prod-qna-question-images.s3.amazonaws.com

The kinetic energy operator and the potential energy operator kinetic energy requires taking into account the momentum operator the potential energy operator is straightforward 4 the hamiltonian becomes: ℝ n → ℝ is called the hamiltonian operator, ℍ, and only very rarely the schrödinger operator. The most important is the hamiltonian, \( \hat{h} \).

Source: quantummechanics.ucsd.edu

The kinetic energy operator and the potential energy operator kinetic energy requires taking into account the momentum operator the potential energy operator is straightforward 4 the hamiltonian becomes: ℝ n → ℝ is called the hamiltonian operator, ℍ, and only very rarely the schrödinger operator. An eigenstate of the momentum operator,ˆp = −i!∂x, with eigenvalue p.

Source: media.howtopronounce.com

The most important is the hamiltonian, \( \hat{h} \). The kinetic energy operator and the potential energy operator kinetic energy requires taking into account the momentum operator the potential energy operator is straightforward 4 the hamiltonian becomes: Time is not an operator in quantum mechanics, it is a parameter, a real number used to describe the way systems change.

Source: i.stack.imgur.com

Now that we have a handle on the position and momentum operators, we can construct a number of other interesting observables from them. The operator, ω 0 σ z /2, represents the internal hamiltonian of the spin (i.e., the energy observable, here given in units for which the reduced planck constant, ℏ = h/(2π) = 1). ℝ n → ℝ is called the hamiltonian operator, ℍ, and only very rarely the schrödinger operator.

Source: www.physicsforums.com

ℝ n → ℝ is called the hamiltonian operator, ℍ, and only very rarely the schrödinger operator.

Source: www.new-npac.org

For a free particle, the plane wave is also an eigenstate of the hamiltonian, hˆ = pˆ2 2m with eigenvalue p2 2m.

Source: www.physicsread.com

You'll recall from classical mechanics that usually,.

Source: s3.studylib.net

You'll recall from classical mechanics that usually,.

Source: www.physicsread.com

Where is plancks constant and the hamiltonian, a hermitian operator.